Сеть GPS-приемников

Определение вариаций полного электронного содержания по данным двухчастотных навигационных спутниковых систем Исследованиям ионосферных геофизических явлений различными методами посвящено огромное количество публикаций. Однако каждый известный науке метод имеет свои недостатки, главными из которых являются невозможность непрерывности и глобальности исследований, и, как следствие, отсутствие статистически значимых наборов экспериментальных данных, которые позволили бы проследить не только морфологические, но и динамические характеристики возбуждаемых ионосферных возмущений: направление перемещения, скорость распространения, положение возможного источника возмущения. Такую возможность впервые предоставляет использование международной наземной сети двухчастотных приемников навигационной системы GPS, насчитывающей к началу 2002 г. не менее 1000 пунктов и поставляющей данные в Internet (http://lox.ucsd.edu), что открывает новую эпоху глобального, непрерывного и полностью компьютеризированного мониторинга ионосферных возмущений различного класса. 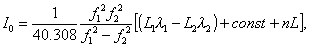Технология GPS предоставляет возможность детектирования волновых возмущений в ионосфере на основе фазовых измерений полного электронного содержания (ПЭС) I(t) в нескольких разнесенных в пространстве двухчастотных приемниках GPS (Hoffmann-Wellenhof et al., 1992): где L₁l₁ и L₂l₁- приращения фазового пути радиосигнала (м); L₁, L₂ - число полных оборотов фазы, а l₁,l₂ - длины волн (м) для частот f₁ и f₂; const - некоторый неизвестный начальный фазовый путь (м); nL - ошибка в определении фазового пути (м). Измерения фазы в системе GPS производятся с высокой степенью точности, при которой ошибка в определении ПЭС при 30 с интервалах усреднения не превышает 10¹⁴ м^-2, хотя начальное значение ПЭС и остается еизвестным. Это позволяет детектировать неоднородности ионизации и волновые процессы в ионосфере в широком диапазоне значений амплитуд (до 10^-4 от суточного изменения ПЭС) и периодов (от суток до 5 мин). Ниже мы будем использовать общепринятую в литературе единицу ПЭС TECU, равную 10¹⁶ м^-2. Первичными данными являются ряды "наклонного" значения 3(ПЭС) I(t), а также соответствующие им ряды значений угла места Θ(t), отсчитываемого от земной поверхности, и азимута α(t) луча зрения на ИСЗ, отсчитываемого от направления на север по часовой стрелке. Эти параметры рассчитываются по разработанной нами программе CONVTEC, которая преобразует полученные по сети Internet стандартные для системы GPS RINEX - файлы. Ряды значений угла места Θ(t) и азимута α(t) луча на ИСЗ используются для определения координат подионосферных точек. В наших работах все результаты получены для углов места Θ(t) больше 30⁰. Для приближенного задания постоянной составляющей ПЭС I_con мы использовали получаемые через Internet (ftp://cddisa.gsfc.nasa.gov) данные соответствующих глобальных карт абсолютного вертикального значения ПЭС в формате IONEX (Mannucci et al., 1998). Для нормировки амплитуды отклика использовалось преобразование наклонного ПЭС в эквивалентное вертикальное значение (Klobuchar, 1986): где R_z - радиус Земли, h_max=300 км высота максимума F₂-слоя. С целью исключения вариаций регулярной ионосферы, а также трендов, внесенных движением спутника, используется процедура удаления тренда с предварительным сглаживанием исходного ряда с временным окном в диапазоне от 40 до 100 мин, подбираемым для каждой реализации ПЭС. Мы определяем пространственно-временные характеристики (скорость и направление перемещения, размеры и форму неоднородностей) ПИВ, используя:

• метод SADM-GPS
• метод определения контраста интерференционной картины (метод Мерсье).
• метод картирования вариаций ПЭС

Метод SADM-GPS Метод SADM-GPS - статистический угломерно-доплеровский метод (Statistical Angle-of-arrival and Doppler Method), разработанный в работах (Афраймович и др., 1997-1999) для определения характеристик динамики ПИВ для GPS-решеток на основе измерения производных ПЭС по времени I'_t(t) и по пространству I'_y(t) и I'_x(t). Это дает возможность установить однозначно ориентацию a(t) волнового вектора K возмущения в диапазоне 0°-360°, а также определить модуль горизонтальной компоненты скорости V_h(t) в каждый момент времени. Изложим кратко последовательность процедур обработки данных. Из большого числа станций GPS выбираются три (А, В, С) пункта, расстояния между которыми не превышают величины порядка половины ожидаемой длины волны l возмущения. Пункт B принимается за центр топоцентрической системы отсчета, ось x которой направлена на восток, ось y - на север. Приемные пункты в данной системе отсчета имеют координаты А(x_A, y_A), В(0,0), С(x_C, y_C). Такая конфигурация приемников GPS представляет собой GPS-решетку с минимально необходимым количеством элементов. В районах с густой сетью GPS-пунктов мы можем получить целый набор GPS-решеток различной конфигурации, что дает возможность проверить достоверность получаемых данных. Ряды значений угла места q_s(t) и азимута a_s(t) луча на ИСЗ используются для определения координат подионосферной точки, а также для вычисления угла места q волнового вектора возмущения K по известному азимуту a. Поскольку расстояние между элементами GPS-решетки (десятки и единицы сотен км) много меньше расстояния до ИСЗ GPS (более 20000 км), геометрия решетки на высоте h_max слоя F₂, для которой рассчитывались координаты подионосферных точек, подобна геометрии решетки на уровне земной поверхности. Горизонтальная проекция фазовой скорости V_h определяется нами при известных координатах пунктов A, B, C решетки по относительным временным сдвигам момента времени t_min максимального отклонения ПЭС. Предварительно измеренные сдвиги подвергаются линейному преобразованию с целью вычисления сдвигов для пунктов, разнесенных относительно центрального пункта на север N и на восток E. Затем вычисляются E- и N - компоненты V_x и V_y, а также направление a в диапазоне углов 0° - 360° и модуль V_h горизонтальной компоненты фазовой скорости: где V_x,V_y - скорости пересечения фазовым фронтом осей x и y. Ориентация a волнового вектора K, совпадающая с азимутом перемещения фазового фронта, вычисляется однозначно в диапазоне 0° - 360° при условии, что arctan(V_x/V_y) вычисляется с учетом знака числителя и знаменателя. Изложенный метод является обобщением широко используемого классического триангуляционного метода разнесенного приема для произвольно расположенных пунктов регистрации сигнала. Однако его непосредственное использование для определения скорости перемещения ПИВ по данным GPS неприемлемо, так как при этом не учитывается перемещение луча зрения на ИСЗ относительно ПИВ в ионосфере. Чтобы учесть этот эффект в условиях интегрального характера измерений ПЭС при трансионосферном зондировании, в первом приближении можно воспользоваться простой моделью эквивалентного "тонкого фазового экрана", расположенного в горизонтальной плоскости на высоте h_max главного максимума электронной концентрации. Это вполне приемлемо, если характерный размер ПИВ сравним со шкалой высот в районе главного максимума, который и дает основной вклад в модуляцию фазы, обусловленной перемещением ПИВ. Для ИСЗ GPS скорость перемещения w точки пересечения луча зрения на ИСЗ с условной плоскостью, выбранной на высоте h_max =300 км (подионосферной точки), становится сравнимой с горизонтальной компонентой V_h скорости перемещения ПИВ, так что учет движения ИСЗ становится необходимым. В работе (Афраймович и др., 1998) разработан метод учета движения ИСЗ с использованием текущей информации об угловых координатах спутников GPS: угле места q_s(t) и азимуте a_s(t). Этот метод приемлем при больших значениях угла места ИСЗ. В работе (Afraimovich et al., 1992) было показано, что для гауссовой модели распределения ионизации амплитуда возмущений ПЭС M(g) определяется ракурсным углом g между векторами K и r, а также отношением длины волны возмущения l к полутолщине максимума ионизации h_d: где q_s - угол места волнового вектора r. Ширина диаграммы направленности достаточно мала, поэтому ракурсное условие: (где a и q - азимут и угол места волнового вектора K ПИВ, a_s и q_s - азимут и угол места направления на ИСЗ) ограничивает число траекторий луча на ИСЗ, для которых возможно уверенное детектирование ПИВ на фоне шумов (вблизи значений углов q=90°). С другой стороны, с использованием ракурсного условия можно определить угол места q волнового вектора K возмущения при известном значении азимута a (Afraimovich et al., 1992). Тогда модуль фазовой скорости V можно определить как: Метод определения контраста интерференционной картины С (Метод Мерсье). Метод позволяет сделать оценку анизотропии наблюдаемой неоднородности. Определяется "контраст" С_N,E двумерной картины (геометрическое место подионосферных точек): при s_Ns_E; при s_Es_N. где s_N, s_E - среднеквадратичные отклонения соответствующих рядов координат N_i и E_i. Эти ряды получены преобразованием исходных рядов N_i' и E_i' путем вращения первоначальной системы координат (N, E) на угол b: В работе (Mercier, 1986) показано, что существует такой угол вращения b₀, при котором отношение C_N,E становится максимальным и равным величине контраста С. Этот параметр характеризует степень анизотропии ПИВ. Угол b₀ в этом случае показывает направление вытянутости, а угол a_c=b₀+p/2 - направление перемещения ПИВ. Метод картирования вариаций ПЭС. В настоящее время активно развиваются спутниковые методы оптического мониторинга верхней атмосферы с высоким пространственным разрешением, что позволяет "визуализировать" некоторые геофизические процессы. Использование данных всемирной сети приемников GPS позволяет разработать аналогичную технологию для глобального мониторинга ионосферных неоднородностей. В [Tsugawa et al., 2007] предложен алгоритм визуализации пространственного распределения (картирования) интенсивности вариаций ПЭС, отражающих неоднородную структуру ионосферы. Для получения пространственного распределения интенсивности вариаций ПЭС используются данные фазовых измерений приемников GPS, расположенных в заданном широтно-долготном регионе. Исходные ряды ПЭС I_ij(t) каждого i-го приемника и каждого j-го НИСЗ фильтруются для выделения колебаний в необходимом диапазоне периодов. Далее для каждого луча «приемник GPS-спутник GPS» рассчитывались координаты подионосферной точки: где R_z – радиус земли; (φ_p, l_p), (φ_B, l_B) – географические координаты (широта и долгота) подионосферной точки и приемника GPS, соответственно; θ_S, α_S – угол места и азимут луча на спутник. В каждый момент времени вариация ПЭС привязывается к подионосферной точке. При большом числе станций получается двумерная картина распределения ПЭС с достаточно высоким разрешением. Впервые нам удалось получить столь высокое пространственное разрешение, что до настоящего времени было не возможно для радиодиапазона. Данный метод был использован для анализа пространственно-временной структуры вариаций ПЭС с периодом 10-30 минут типа волновых пакетов [Afraimovich et al., 2009]. Временное окно для сглаживания было выбрано 2 минуты, для удаления тренда – 30 мин. На рисунке показаны типичные волновые пакеты в ночное время после прохождения солнечного терминатора 13 июня 2008 г., 14:00 UT (21:00 LT); спутник PRN19. Амплитуда вариаций ПЭС dI(t) не превышает 0.1 TECU (1016 м-2). Линиями отмечено положение максимумов волн пакета. Вдоль Японии укладывается не менее 10 волн с длиной порядка 80 км. Картирование вариаций типа волновых пакетов с периодом 10-30 минут в ночное время после прохождения солнечного терминатора 13 июня 2008 г., 14:00 UT; спутник PRN19. Для исследования общего состояния ионосферы был разработан новый обобщенный параметр Глобальное электронное содержание (ГЭС) [Афраймович и др., 2006]. Глобальное электронное содержание Метод расчета ГЭС основан на использовании технологии построения глобальных карт ПЭС. Для каждого момента времени с двухчасовым временным разрешением из файлов IONEX известны значения абсолютного вертикального ПЭС I^ij_AV, где индексы i, j отмечают координаты (широту и долготу) GIM-ячейки. Глобальное электронное содержание G вычисляется путем суммирования по всем GIM-ячейкам значений ПЭС для каждой ячейки, умноженных на площадь GIM-ячейки S^ij: Для удобства анализа ГЭС предложена единица измерений GECU=10³² электронов. Точность определения ПЭС в одной GIM-ячейке варьируется от 5% до 20%. Поскольку усреднение независимых значений ПЭС осуществляется по всему земному шару с общим количеством GIM-ячеек, равным 5184, точность оценки ГЭС на один-два порядка выше. Это позволяет обнаружить колебания и тренды ГЭС весьма незначительной амплитуды, что невозможно при анализе ПЭС в отдельно взятой GIM-ячейке. Сравнительный анализ показал, что получаемые результаты не зависят от того, IONEX-файлы какой лаборатории используются для расчета ГЭС. Величина и вариации ГЭС обусловлены тремя основными факторами: солнечная активность, процессы в магнитосфере, процессы в нейтральной атмосфере. Таким образом, этот обобщенный ионосферный параметр может быть использован как индекс, отражающий состояние околоземного космического пространства. Кроме того, данные ГЭС могут применяться для решения обратных задач, например, получения количественных характеристик потока ультрафиолетового излучения Солнца и пр. Несколько важных ограничений такого анализа:

1. Термин ГЭС мы используем на том основании, что на картах GIM представлена вся поверхность земного шара. В действительности оценка полного электронного содержания в областях ионосферы вокруг географических полюсов дана на этих картах весьма приближенно. Для данных областей более представительными являются карты NOR, выставляемые группой Jakowski на сайте http://www.kn.nz.dlr.de/daily/tec-np/. Однако вклад высокоширотных областей в ГЭС существенно ниже вклада средних и низких широт, так что в первом приближении рассчитанная величина G достаточно близка к общему количеству электронов вокруг Земли.
2. Расчет числа электронов для отдельной ячейки GIM фактически проводится в пределах трубки неизменного диаметра, т.е. не учитывается сферическая расходимость. Погрешность вычисления абсолютного значения ГЭС в результате составляет ~10-20%. Следует отметить, что указанная систематическая ошибка определения полного числа электронов в околоземном пространстве по формуле в основном влияет только на абсолютное значение ГЭС, а не на форму и характер вариаций ГЭС.

Список цитируемой литературы

1. Hofmann-Wellenhoff B., Lichtenegger H. and Collins J., Global Positioning System: Theory and Practice, Springer-Verlag Wien, New York, 1992
2. Mannucci, A.J., C.M. Ho, U.J. Lindqwister, T.F. Runge, B.D. Wilson and D.N. Yuan. A global mapping technique for GPS-drived ionospheric TEC measurements. Radio Science, 1998. V 33. N 8. P. 565-582.
3. Klobuchar J. A., Ionospheric time-delay algorithm for single-frequency GPS users, IEEE Transactions on Aerospace and Electronics System, 1986, V. 23, N 3, P. 325.
4. Afraimovich E. L. Statistical angle-of-arrival and doppler method (SADM) for determining characteristics of the dynamics of the transionospheric radio signal interference pattern. Acta Geod. Geoph. Hung., 1997. V. 32. N 3-4. P. 461-468.
5. Afraimovich E. L., Palamartchouk K. S., and Perevalova N. P. GPS radio interferometry of travelling ionospheric disturbances. J. Atmos. Sol. Terr. Phys., 1998. V. 60. N 12. P. 1205-1223.
6. Afraimovich E. L., Boitman O. N., Zhovty E.I., Kalikhman A.D., and Pirog T.G.. Dynamics and anisotropy of traveling ionospheric disturbances as deduced from transionospheric sounding data. Radio Science, 1999. V. 34, N 2, P. 477 - 487.
7. Afraimovich E. L., Terekhov A.I.,.Udodov M.Yu, and Fridman S.V., Refraction distortions of transionospheric radio signals caused by changes in a regular ionosphere and by travelling ionospheric disturbances. J. Atmos. Terr. Phys., 1992. V. 54. P. 1013 - 1020.
8. Mercier, C. Observations atmospheric gravity waves by radiointerferometry. J. Atmos. Terr. Phys., 1986. V. 48, P. 605-624.
9. T. Tsugawa, Y. Otsuka, A.J. Coster, A. Saito, Medium-scale traveling ionospheric disturbances detected with dense and wide TEC maps over North America, Geophys. Res. Lett., 2007, 34, L22101, doi:10.1029/2007GL031663.
10. E.L. Afraimovich, I.K. Edemskiy, S.V. Voeykov, Yu.V. Yasyukevich, I.V. Zhivetiev. The first GPS-TEC imaging of the space structure of MS wave packets excited by the solar terminator. Annales Geophysicae.-2009.-V.27.-P.1521-1525.
11. Э.Л. Афраймович, Э.И. Астафьева, И.В. Живетьев. Солнечная активность и глобальное электронное содержание. Доклады Академии Наук. Геофизика, 2006, Т. 409, №3, С.399-402.